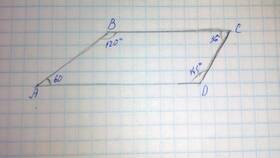
Сумма внутренних углов выпуклого четырехугольника является важной характеристикой этой геометрической фигуры. Рассмотрим подробнее это свойство и его доказательство.
Содержание
Основное свойство
Для любого выпуклого четырехугольника сумма внутренних углов равна:
| Формула | 360° |
| Графическое представление | ∠A + ∠B + ∠C + ∠D = 360° |
Доказательство теоремы
Существует несколько способов доказать это свойство:
Метод разбиения на треугольники
- Провести диагональ в четырехугольнике
- Разбить фигуру на два треугольника
- Сумма углов каждого треугольника - 180°
- Общая сумма: 180° × 2 = 360°
Метод внешних углов
- Продлить все стороны четырехугольника
- Рассмотреть сумму внешних углов
- Использовать свойство суммы внутренних и внешних углов
Частные случаи четырехугольников
| Тип четырехугольника | Особенности углов |
| Прямоугольник | Все углы равны 90° (4 × 90° = 360°) |
| Ромб | Противоположные углы равны |
| Параллелограмм | Противоположные углы равны, соседние дополняют до 180° |
| Трапеция | Сумма углов при каждой боковой стороне равна 180° |
Практическое применение
Знание суммы углов четырехугольника позволяет:
- Решать геометрические задачи на вычисление неизвестных углов
- Проверять правильность построения фигур
- Конструировать объекты в архитектуре и дизайне
- Создавать компьютерные модели
Пример задачи:
В четырехугольнике три угла равны 80°, 95° и 110°. Найдите четвертый угол.
Решение: 360° - (80° + 95° + 110°) = 75°
Сумма внешних углов
Для выпуклого четырехугольника сумма внешних углов также составляет:
- 360° (при обходе по часовой стрелке или против)
- Каждый внешний угол дополняет внутренний до 180°
Важно:
Данное свойство выполняется только для выпуклых четырехугольников. Для невыпуклых сумма углов также равна 360°, но доказательство требует особого подхода.