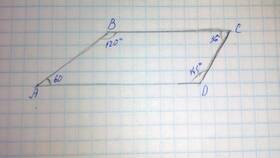
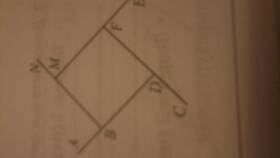
Свойство четырехугольника иметь сумму внутренних углов равной 360 градусам является фундаментальным в евклидовой геометрии. Рассмотрим математическое обоснование этого факта и различные методы доказательства.
Содержание
Геометрическое доказательство
Любой четырехугольник можно разделить на два треугольника:
| Фигура | Сумма углов |
| Треугольник 1 | 180° |
| Треугольник 2 | 180° |
| Общая сумма | 180° + 180° = 360° |
Алгоритм разделения четырехугольника
- Выбрать любые две несмежные вершины
- Провести диагональ между ними
- Получить два треугольника
- Сложить суммы их углов
Алгебраическое доказательство
Для выпуклого n-угольника сумма углов вычисляется по формуле:
- S = (n - 2) × 180°
- Для четырехугольника (n=4): S = (4-2) × 180° = 360°
Обобщение для многоугольников
| Фигура | Формула | Сумма углов |
| Треугольник | (3-2)×180° | 180° |
| Четырехугольник | (4-2)×180° | 360° |
| Пятиугольник | (5-2)×180° | 540° |
Доказательство через внешние углы
Свойство внешних углов многоугольника:
- Сумма внешних углов любого многоугольника равна 360°
- Каждый внутренний угол дополняет внешний до 180°
- Для n вершин: n×180° - сумма внутренних углов = 360°
- Для четырехугольника: 4×180° - 360° = 360°
Визуализация метода
- Представить обход четырехугольника по периметру
- На каждом повороте изменяется направление на величину внешнего угла
- После полного обхода направление возвращается к исходному
- Сумма всех поворотов составляет 360°
Историческая справка
Это свойство было известно еще древнегреческим математикам и содержится в "Началах" Евклида. Оно является следствием аксиом евклидовой геометрии и не зависит от формы четырехугольника, применимо как к выпуклым, так и к вогнутым четырехугольникам.